Hexagon
Pronunciation: /ˈhɛk.səˌgɒn/ Explain
|
A hexagon is a six sided polygon. The sides of a hexagon are straight line segments. A hexagon is a planar figure, a figure that exists in a plane. A hexagon can be concave or convex. If a convex hexagon is equilateral (the sides are the same length), then the hexagon is a regular hexagon. |
Article Index
HexagonRegular Hexagon
Parts of a Regular Hexagon
Formulas for a Regular Hexagon
How to Construct a Regular Hexagon From its Circumcircle
How to Construct the Center, Incircle and Circumcircle of a Regular Hexagon
Tessellations of a Regular Hexagon
Natural and Manufactured Hexagons
Regular hexagon
A regular hexagon is a six sided, equilateral, convex polygon. An equilateral polygon has sides that are all the same length. No line segment drawn between any two points in a convex figure leaves the figure.
|
Click on the blue points and drag them to change the figure. When is the length of a side different from the length of the circumradius? |
| Manipulative 1 - Regular Hexagon Created with GeoGebra. |
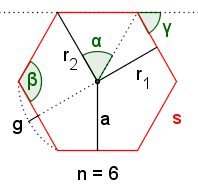
Parts of a regular hexagon
- side or edge: One of the line segment that makes up hexagon. The length of a side of a regular hexagon will be denoted s in this article.
- vertex: Where two of the sides of the hexagon meet.
- interior: The area inside the hexagon.
- exterior: The area outside the hexagon.
- boundary: The sides and vertices of the hexagon.
- center: The point at the middle of the hexagon. The center of a regular hexagon can be found at the intersection of the perpendicular bisectors of any two sides. See How to Construct the Center, Incircle and Circumcircle of a Regular Hexagon. The center of a regular hexagon is also its centroid.
- incircle: A circle whose center is at the center of a regular hexagon that touches each side of the hexagon once. In this article, the radius of the incircle will be denoted r1.
- circumcircle: A circle whose center is at the center of a regular hexagon that intersects each of the vertices of the regular hexagon. In this article, the radius of the circumcircle will be denoted r2.
- apothem: A line segment from the center of a regular hexagon to the midpoint of one of the sides. The length of the apothem is the same as the radius of the incircle and is denoted (r1).
- sagitta: A line segment from the center of a side to the edge of the circumcircle of a regular hexagon that is collinear with the apothem.
- central angle:: The angle between two line segments extending from the center of the regular hexagon to two adjacent vertices. The central angle of a regular hexagon is always 72°.
- interior angle: The angle between two adjacent sides. The interior angles of a regular hexagon always measure 120°. The sum of the measures of interior angles of any convex hexagon is 720°.
- exterior angle: The angle between the extended side of a regular hexagon and an adjacent side. The exterior angles of a regular hexagon always measure 60°.
Formulas for a regular hexagon
| Illustration | Formula | Description |
|---|---|---|
 |
n = 6 | number of sides |
| s | length of a side | |
| p = 6s | perimeter | |
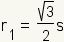 | radius of the incircle | |
| r2 = s | radius of the circumcircle | |
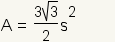 | area of the hexagon | |
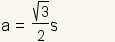 | length of the apothem | |
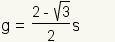 | length of the sagitta | |
| α = 72° | measure of the central angles | |
| β = 120° | measure of the interior angles | |
| γ = 60° | measure of the exterior angles | |
| Table 1: Formulas for a regular hexagon. | ||
How to Construct a Regular Hexagon from its Circumcircle
| Step | Illustration | Description and Justification |
|---|---|---|
| 1 | 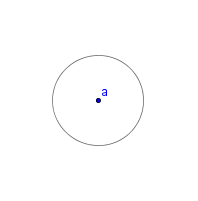 |
Draw a circle. Label the center of the circle a. This is given. |
| 2 | 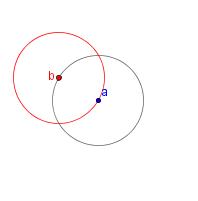 |
Draw a circle with the center on the circumference of circle a that is the same radius as circle a. Label the center of this circle b. |
| 3 | 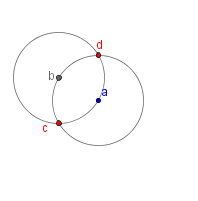 |
Label the intersections of the circles c and d. |
| 4 | 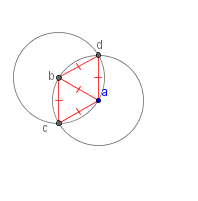 |
Draw line segments ab, ac, ad, bc and bd. Note that all of these line segments are radii of congruent circles. This means that they are all the same length. So triangles Δabc and Δabd are equilateral triangles, triangles whose sides have the same measure. The angles of equilateral triangles also have the same measure. Therefore, triangles Δabc and Δabd are congruent by the SAS Congruence Theorem. |
| 5 | 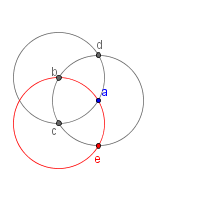 |
Draw another circle with the same radius as a with a center at c. Label the new intersection of circle c and circle a as e. |
| 6 | 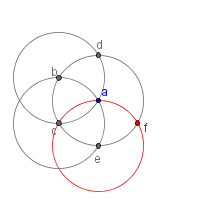 |
Draw another circle with the same radius as a with a center at e. Label the new intersection of circle e and circle a as f. Note that by the same arguments that were used in step 5, triangles Δabc and Δace are congruent equilateral triangles. |
| 7 | 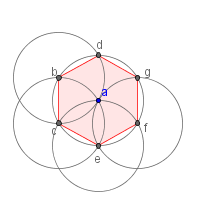 |
Continue the pattern until circles with centers at b, c,
d, e, f and g are drawn. We know this
is a regular hexagon because
|
| Table 2: How to construct a regular hexagon from its circumcircle. | ||
How to Construct the Center, Incircle and Circumcircle of a Regular Hexagon
| Step | Illustration | Discussion and Justification |
|---|---|---|
| 1 |  |
The center of a regular hexagon is at the point of concurrency of perpendicular bisectors of any two sides that are not opposite each other. |
| 2 | 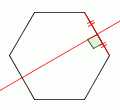 |
Draw the perpendicular bisector of any side. |
| 3 | 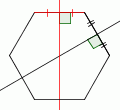 |
Draw the perpendicular bisector of any other side that is not opposite the side you used in step 2. |
| 4 | 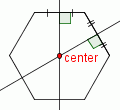 |
Label the intersection of the two perpendicular bisectors as 'center'. |
| 5 | 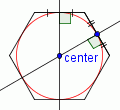 |
Draw a circle with a center at the point labeled 'center' and the edge at a point where a perpendicular bisector intersects a side. This is the incircle. |
| 6 | 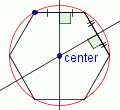 |
Draw a circle with a center at the point labeled 'center' and the edge at any vertex. This is the circumcircle. |
| Table 3 - How to construct the center, incircle and circumcircle of a regular hexagon | ||
Tessellations of a Hexagon
A tessellation of one or more polygon is an arrangement of those polygons that fills a plane. The are a number of tessellations that use hexagons. Most of the tessellations shown here use regular hexagons.
 |
 |
| A regular tessellation of a hexagon. Three hexagons are around each vertex. | A trihexagonal tiling. Each vertex has a regular hexagon, an equilateral triangle, a regular hexagon and an equilateral triangle. |
| Table 4: tessellations of a hexagon | |
Natural and Manufactured Hexagons
References
- McAdams, David E.. All Math Words Dictionary, hexagon. 2nd Classroom edition 20150108-4799968. pg 90. Life is a Story Problem LLC. January 8, 2015. Buy the book
More Information
- McAdams, David E.. Polygon. allmathwords.org. Life is a Story Problem LLC. 10/22/2010.
Cite this article as:
McAdams, David E. Hexagon. 4/22/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/h/hexagon.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
- Hexagonal Pavement Tiles: Claudine Rodriguez, https://commons.wikimedia.org. This file is licensed under the Creative Commons Attribution 2.0 Generic license. https://commons.wikimedia.org/wiki/File:Hexagon_-_by_Claudine_Rodriquez.jpg.
- Hexagonal Cloud Formation on the North Pole of Saturn: NASA/JPL/University of Arizona, https://www.jpl.nasa.gov. Public domain. https://www.jpl.nasa.gov/news/news.php?release=2007-034.
- Hexagonal Mirror Array: NASA, https://mix.msfc.nasa.gov. Public domain. https://mix.msfc.nasa.gov/abstracts.php?p=2458.
- Carbon-36 Fullerene Molecule: US Department of Energy, http://www.lbl.gov. Public domain. http://www.lbl.gov/Science-Articles/Archive/carbon-36-superconductor.html.
- Hexagonal Basalt Formation: US Department of Interior, Bureau of Land Management, https://www.blm.gov. Public domain.
- Hexagonal Honeycomb. Unknown.
Revision History
4/22/2019: Update equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/16/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
10/22/2010: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License